-
阐述
是离散 Fourier 变换的量子版本。
对于由 个量子位构成的向量,其状态数为 ,定义 次单位根 ,则 阶张量积态 的正向变换为
相应的逆向变换为
-
实例
-
性质
-
相关内容
该变换可以由 Hadamard 门和控制旋转门 实现,其中
注意到 ,我们可以设计出如下电路:
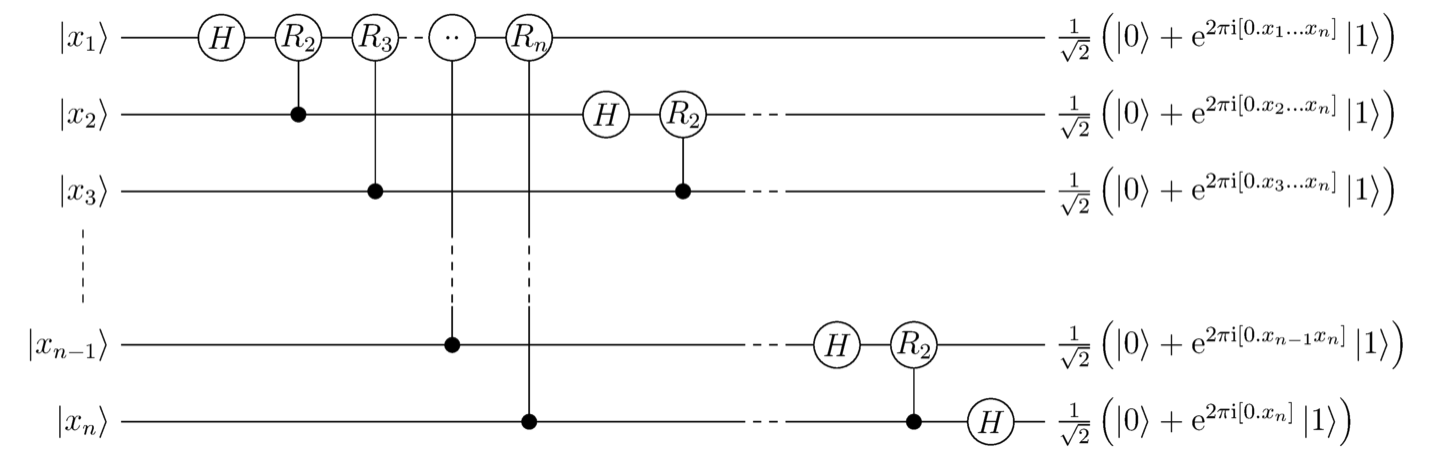
注意,输入和输出的顺序是相反的。
-
参考文献
是离散 Fourier 变换的量子版本。
对于由 个量子位构成的向量,其状态数为 ,定义 次单位根 ,则 阶张量积态 的正向变换为
相应的逆向变换为
该变换可以由 Hadamard 门和控制旋转门 实现,其中
注意到 ,我们可以设计出如下电路:

注意,输入和输出的顺序是相反的。